We propose Hyper-Dimensional Function Encoding (HDFE).
Given samples of a continuous object (e.g. a function),
HDFE produces an explicit vector representation of the given object,
invariant to the sample distribution and density.
Sample distribution and density invariance enables HDFE to consistently encode continuous objects regardless of their sampling,
and therefore allows neural networks to receive continuous objects as inputs for machine learning tasks,
such as classification and regression.
Besides, HDFE does not require any training and is proved to map the object into an organized embedding space,
which facilitates the training of the downstream tasks.
In addition, the encoding is decodable,
which enables neural networks to regress continuous objects by regressing their encodings.
Therefore, HDFE serves as an interface for processing continuous objects.
Application I: Function-to-Function Mapping
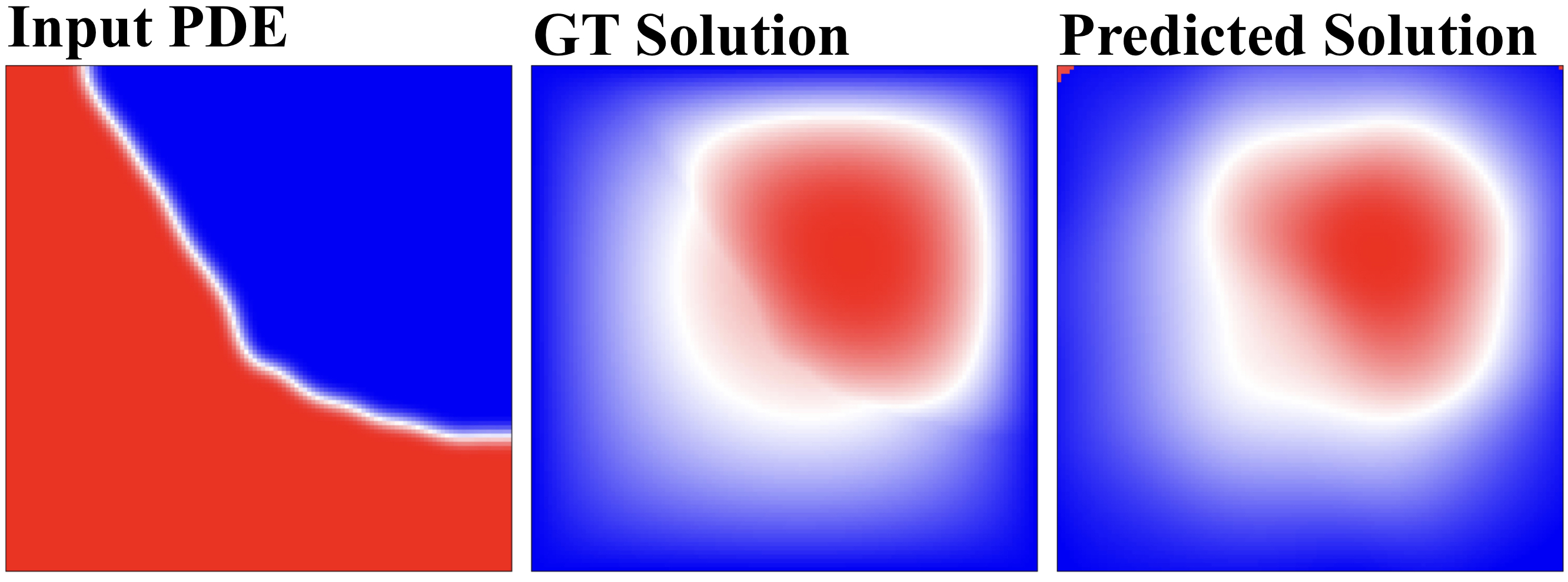
Figure 1. We evaluate our HDFE on function-to-function mapping tasks, specifically mapping partial differential equations (PDEs) to their solutions.
We demonstrate that HDFE can accurately predict the solutions of PDEs, even when the input PDEs are sampled under different resolutions.
Application II: Function Attribute Prediction

Table 1. HDFE outperforms the PointNet baseline in the normal estimation task. We compare the vanilla HDFE with the PCPNet, which is a vanilla PointNet architecture.
We replace the PointNet with our HDFE appended with a deep complex network. Such replacement yields significantly higher performance.

Table 2. HDFE, as a plug-in module, improves the SOTA baseline significantly. We integrate HDFE into the HSurf-Net, which is the state-of-the-art PointNet-based normal estimator.
Such integration yields significantly higher performance.
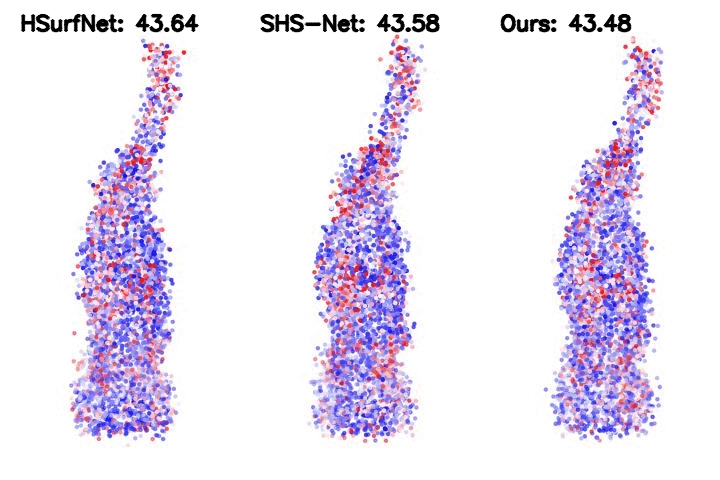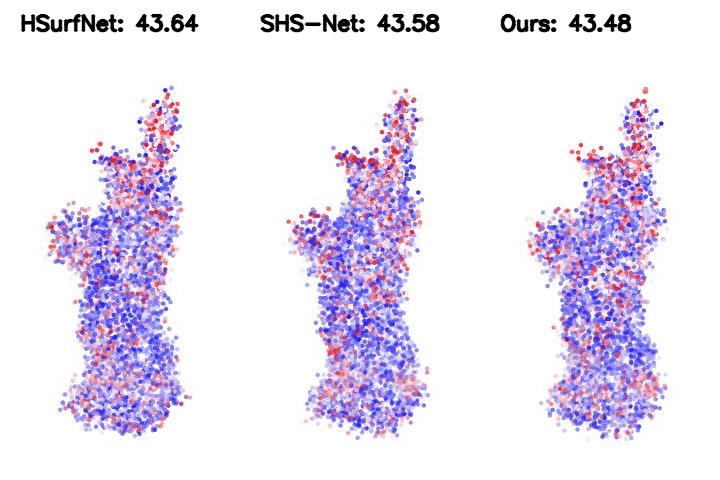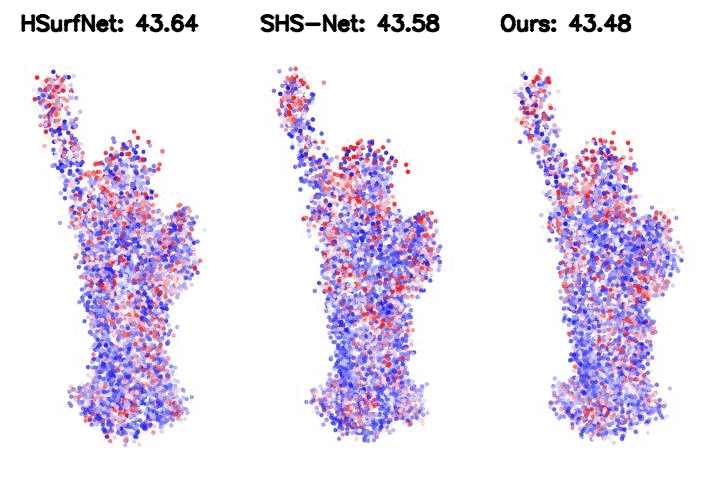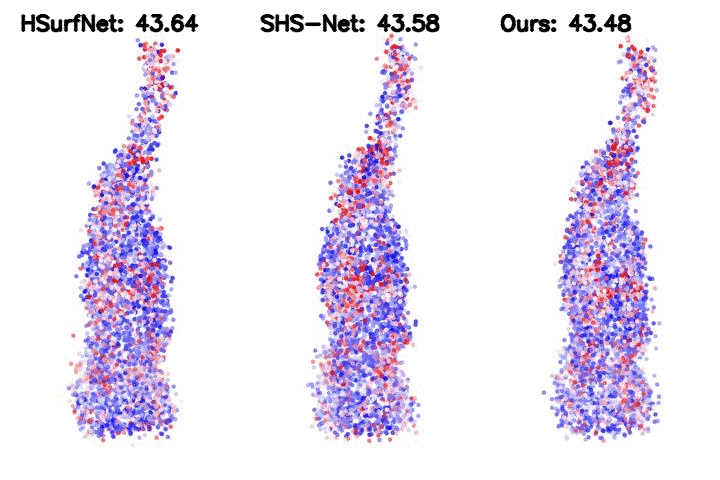
Figure 2. Point cloud normal estimation error visualization. The metric is the root mean square error (RMSE) of the normal estimation.





