We investigate how machine learning schemes known as a Reservoir Computers (RCs) learn concepts such as 'similar' and 'different', and other relationships between pairs of inputs and generalize these concepts to previously unseen types of data. RCs work by feeding input data into a high dimensional dynamical system of neuron-like units called a 'reservoir' and using regression to train 'output weights' to produce the desired response. We study two RC architectures, that broadly resemble neural dynamics. We show that an RC that is trained to identify relationships between imagepairs drawn from a subset of handwritten digits (0-5) from the MNIST database generalizes the learned relationships to images of handwritten digits (6-9) unseen during training. We consider simple relationships between the input image pair such as: same digits (digits from the same class), same digits but one is rotated 90 degrees, same digits but one is blurred, different digits, etc. In this dataset, digits that are marked the 'same' may have substantial variation because they come from different handwriting samples. Additionally, using a database of depth maps of images taken from a moving camera, we show that an RC trained to learn relationships such as 'similar' (e.g., same scene, different camera perspectives) and 'different' (different scenes) is able to generalize its learning to visual scenes that are very different from those used in training. RC being a dynamical system, lends itself to easy interpretation through clustering and analysis of the underlying dynamics that allows for generalization. We show that in response to different inputs, the high-dimensional reservoir state can reach different attractors (i.e. patterns), with different attractors representative of corresponding input-pair relationships. We investigate the attractor structure by clustering the high dimensional reservoir states using dimensionality reduction techniques such as Principal Component Analysis (PCA). Thus, as opposed to training for the entire high dimensional 1 reservoir state, the reservoir only needs to learn these attractors (patterns), allowing it to perform well with very few training examples as compared to conventional machine learning techniques such as deep learning. We find that RCs can not only identify and generalize linear as well as non-linear relationships, but also combinations of relationships, providing robust and effective image-pair classification. We find that RCs perform significantly better than state-of-the-art neural network classification techniques such as convolutional and deep Siamese Neural Networks (SNNs) in generalization tasks both on the MNIST dataset and scenes from a moving camera dataset. Using small datasets, our work helps bridge the gap between explainable machine learning and biologically-inspired learning through analogies and points to new directions in the investigation of learning processes.
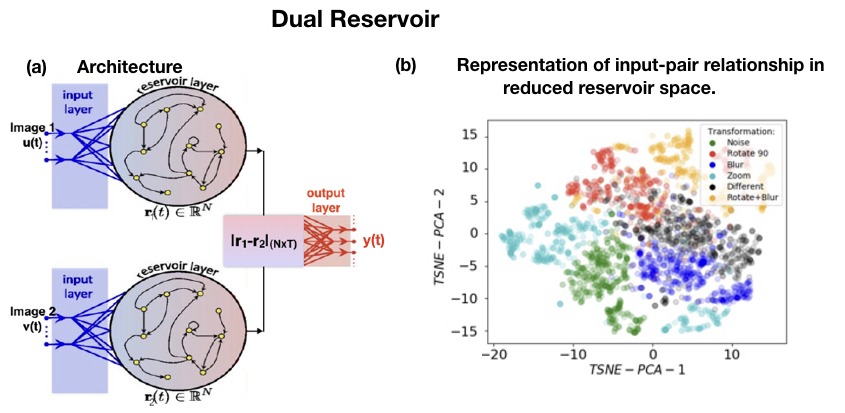
Fig. 1. Dual reservoir architecture with input state of the two images at time t denoted by u(t) and v(t),
reservoir state at a single time by r (t) and output state by y (t). The two input images are from the same category/label with a relationship, with one or more transformations applied to one of the images. The transformations considered here are noise, rotate 90, scale, blur, different. (b) A representation of the resulting high dimensional reservoir state in a lower dimensional space (obtained through Principal Component Analysis and t-Distributed Stochastic Neighbor Embedding) for different transformations. Automatic clustering of reservoir representation occurs, analogous to attractors in a dynamical system such as a reservoir computer.