Cooking recipes are challenging to translate to robot plans as they feature rich linguistic complexity, temporally-extended interconnected tasks, and an almost infinite space of possible actions. Our key insight is that combining a source of cooking domain knowledge with a formalism that captures the temporal richness of cooking recipes could enable the extraction of unambiguous, robot-executable plans. In this work, we use Linear Temporal Logic (LTL) as a formal language expressive enough to model the temporal nature of cooking recipes. Leveraging a pretrained Large Language Model (LLM), we present Cook2LTL, a system that translates instruction steps from an arbitrary cooking recipe found on the internet to a set of LTL formulae, grounding high-level cooking actions to a set of primitive actions that are executable by a manipulator in a kitchen environment. Cook2LTL makes use of a caching scheme that dynamically builds a queryable action library at runtime. We instantiate Cook2LTL in a realistic simulation environment (AI2-THOR), and evaluate its performance across a series of cooking recipes. We demonstrate that our system significantly decreases LLM API calls (−51%), latency (−59%), and cost (−42%) compared to a baseline that queries the LLM for every newly encountered action at runtime.

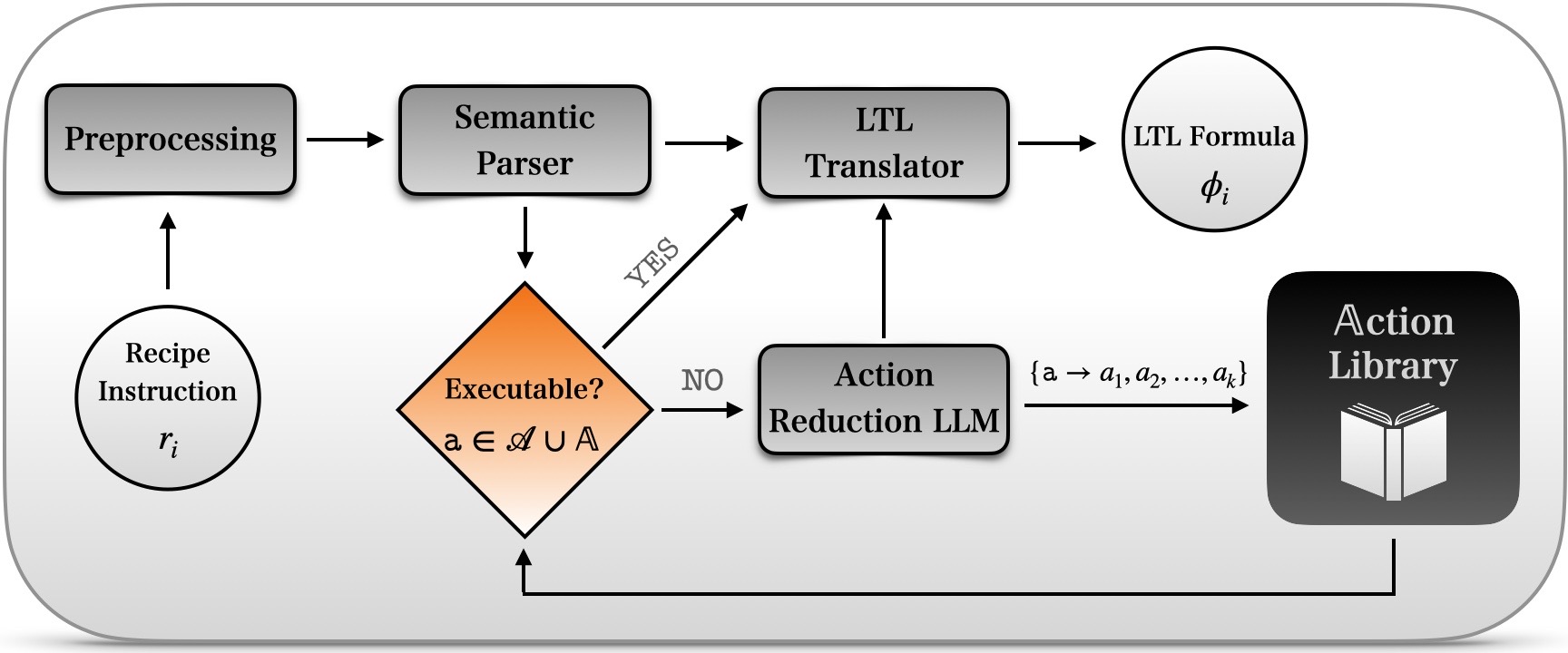
Cook2LTL System: The input instruction \(r_i\) is first preprocessed and then passed to the semantic parser, which extracts meaningful chunks corresponding to the categories \(\mathcal{C}\) and constructs a function representation \(\mathtt{a}\) for each detected action. If \(\mathtt{a}\) is part of the action library \(\mathbb{A}\), then the LTL translator infers the final LTL formula \(\phi\). Otherwise, the action is reduced to a sequence of lower-level admissible actions \(\{a_1,a_2,\dots a_k\}\) from \(\mathbb{A}\), and the reduction policy is cached to \(\mathbb{A}\) for future use. The LTL translator then yields the final LTL formulae based on the derived actions.

The first step of Cook2LTL is a semantic parser that extracts salient categories \(\mathcal{C}\)towards building a function representation in the form of \(\mathtt{a}=\mathtt{Verb(What?,Where?,How?,Time,Temperature)}\) for every detected action. To this end, we annotate a subset (100 recipes) of the Recipe1M+ dataset and fine-tune a pre-trained spaCy NER BERT model to predict these categories in unseen recipes at inference. To annotate the recipes we used the Brat annotation tool (installation instructions). To fill in context-implicit parts of speech (POS), we use ChatGPT or manually inject them into the sentence.

Inspired by ProgPrompt, Cook2LTL uses an LLM prompting scheme to reduce a high-level cooking action, e.g. \(\mathtt{boil (eggs)}\), to a series of primitive manipulation actions. The prompt consists of an \(\mathtt{import}\) statement of the primitive action set and example function definitions of similar cooking tasks. The key benefit of using this paradigm is that it constrains the output action plan of the LLM to only include subsets of the available primitive actions. We extend this prompting scheme by reusing derived LLM policies. In this case, the action \(\mathtt{boil}\) is added to future \(\mathtt{import}\) statements in the input prompt, enabling the model to invoke the derived \(\mathtt{boil}\) function which is now considered given to the system.

Every time that we query the LLM for action reduction, we cache \(\mathtt{a}\) and its action reduction policy to an action library \(\mathbb{A}\) for future use through a dictionary lookup manner. At runtime, a new action \(\mathtt{a}\) is now checked against both \(\mathcal{A}\) and \(\mathbb{A}\). If \(\mathtt{a}\in\mathbb{A}\), which means that \(\mathtt{Verb}\) from \(\mathtt{a}\) matches the \(\mathtt{Verb}\) from an action \(\mathtt{a}_\mathbb{A}\) in \(\mathbb{A}\) and the parameter types match (e.g. both actions have \(\mathtt{What?}\) and \(\mathtt{Where?}\) as parameters), then \(\mathtt{a}\) is replaced by \(\mathtt{a}_\mathbb{A}\) and its LLM-derived sub-action policy, and passed to the subsequent LTL Translation step.

We assume the following specification pattern for executing a set of implicitly sequential actions \(\{\mathtt{a}_1,\mathtt{a}_2,\dots,\mathtt{a}_n\}\) found in a recipe instruction step: \(\mathcal{F}(\mathtt{a}_1\wedge \mathcal{F}(\mathtt{a}_2\wedge\dots\mathcal{F}\mathtt{a}_n)))\). We scan every chunk extracted from the NER module for instances of conjunction, disjunction, or negation, and produce an initial LTL formula \(\phi\) using the above equation and the operators \(\mathcal{F},\wedge,\vee,\lnot\). Following the action reduction module, we substitute any reduced actions to the initial formula \(\phi\). For example, if \(\mathtt{a}\rightarrow\{a_1,a_2,\dots,a_k\}\), then \(\mathcal{F}\mathtt{a}\) is converted to the formula \(\mathcal{F}(a_1\wedge\mathcal{F}(a_2\wedge\dots\mathcal{F}a_n)))\). In cases where the \(\mathtt{Time}\) parameter includes explicit sequencing language, the LLM has been prompted to return a \(\mathtt{wait}\) function, which is parsed into the \(\mathcal{U}\) : \(\mathtt{until}\) operator and substituted in \(\phi\).

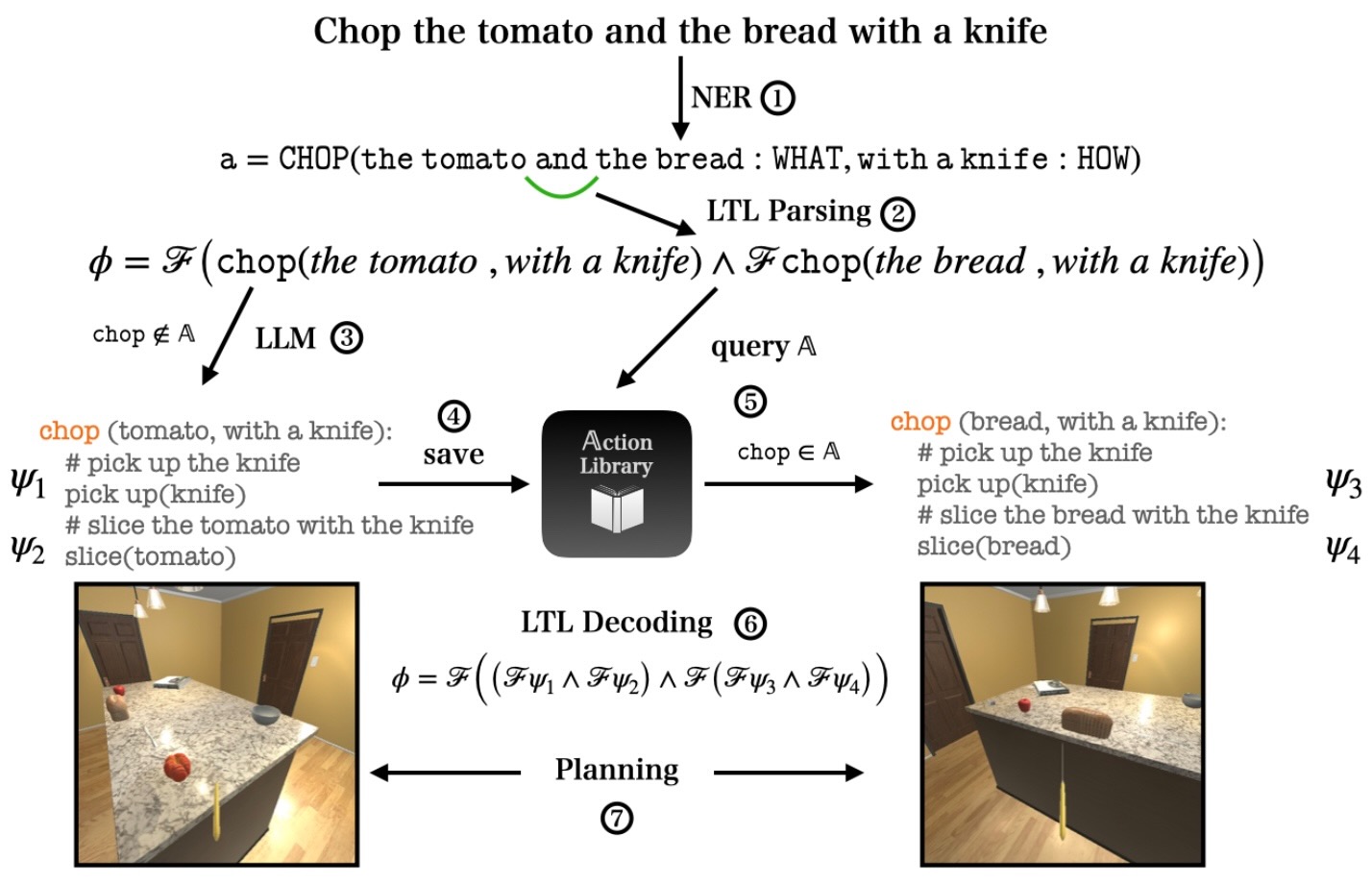
We demonstrate the performance of Cook2LTL in a simulated AI2-THOR kitchen environment. In this example, the NER module produces an action representation \(\mathtt{a}\) given a recipe step, and is then parsed to an initial formula \(\phi\). Upon encountering an unknown action \(\mathtt{chop}\), it queries the LLM for a policy which yields subformulae \(\psi_1\) and \(\psi_2\). This policy is saved to the action library \(\mathbb{A}\). Next, when encountering again the now known action \(\mathtt{chop}\), the system re-uses the cached policy substituting its corresponding parameters and yielding subformulae \(\psi_3\) and \(\psi_4\). All produced subformulae are then substituted and decoded to the final formula \(\phi\) that is passed to a minimal planner in the AI2-THOR environment.

Angelos Mavrogiannis, Christoforos Mavrogiannis, Yiannis Aloimonos