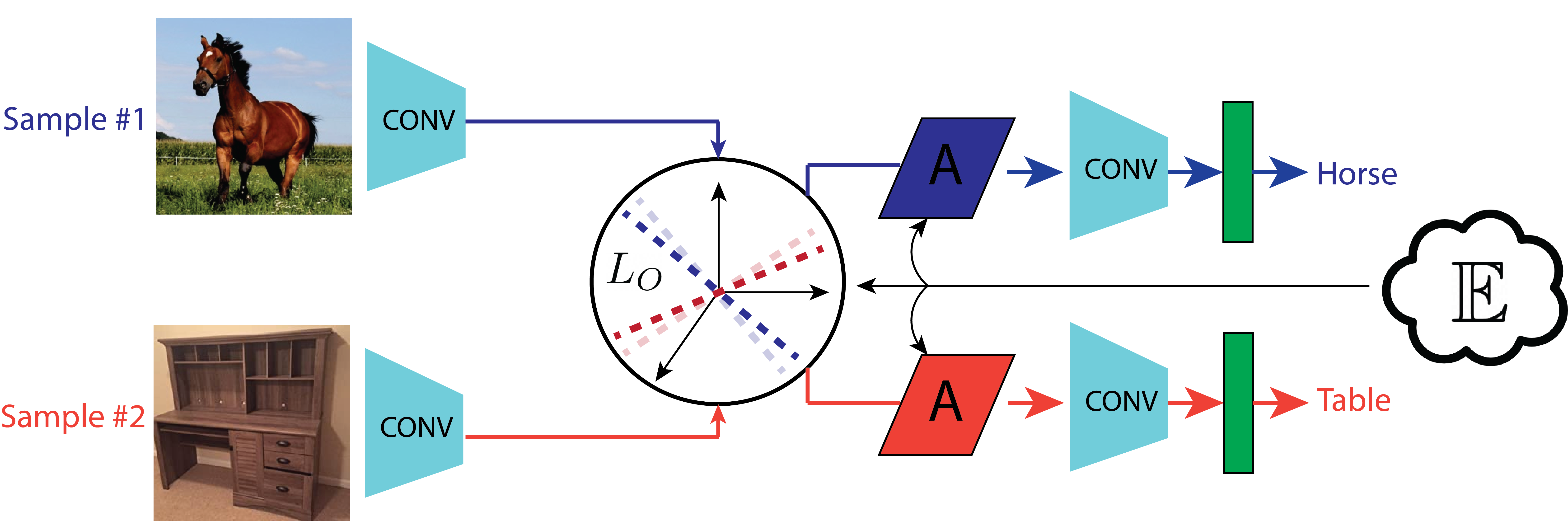
Figure 3: MVF structure. As training involves a contrastive loss between samples belonging to different contexts, the base network is shown twice in the figure: on the top when fed with a horse image, and on the bottom when fed with a desk image. Affine transformations (linear transformations) are inserted into a conventional CNN architecture. These affine transformations modulate feature representations at injection levels (network levels over which affine transformations are applied) in accordance with high level context expectations (E}). A contrastive loss (Lo) is inserted to put pressure on the network to help separate feature representations at the injection levels according to context, better enabling affine manipulation. During training, samples from different contexts are fed through the network. The context expectations determine the behavior of Lo and the selection of appropriate affine transformations.

Feedback plays a prominent role in biological vision, where perception is modulated based on agents' continuous interactions with the world, and evolving expectations and world model. We introduce a novel mechanism which modulates perception in Convolutional Neural Networks (CNNs) based on high level categorical expectations: Mid-Vision Feedback (MVF). MVF associates high level contexts with linear transformations. When a context is "expected" its associated linear transformation is applied over feature vectors in a mid level of a CNN. The result is that mid-level network representations are biased towards conformance with high level expectations, improving overall accuracy and contextual consistency. Additionally, during training mid-level feature vectors are biased through introduction of a loss term which increases the distance between feature vectors associated with different contexts. MVF is agnostic as to the source of contextual expectations, and can serve as a mechanism for top down integration of symbolic systems with deep vision architectures. We show the superior performance of MVF to post-hoc filtering for incorporation of contextual knowledge, and show superior performance of configurations using predicted context (when no context is known a priori) over configurations with no context awareness.

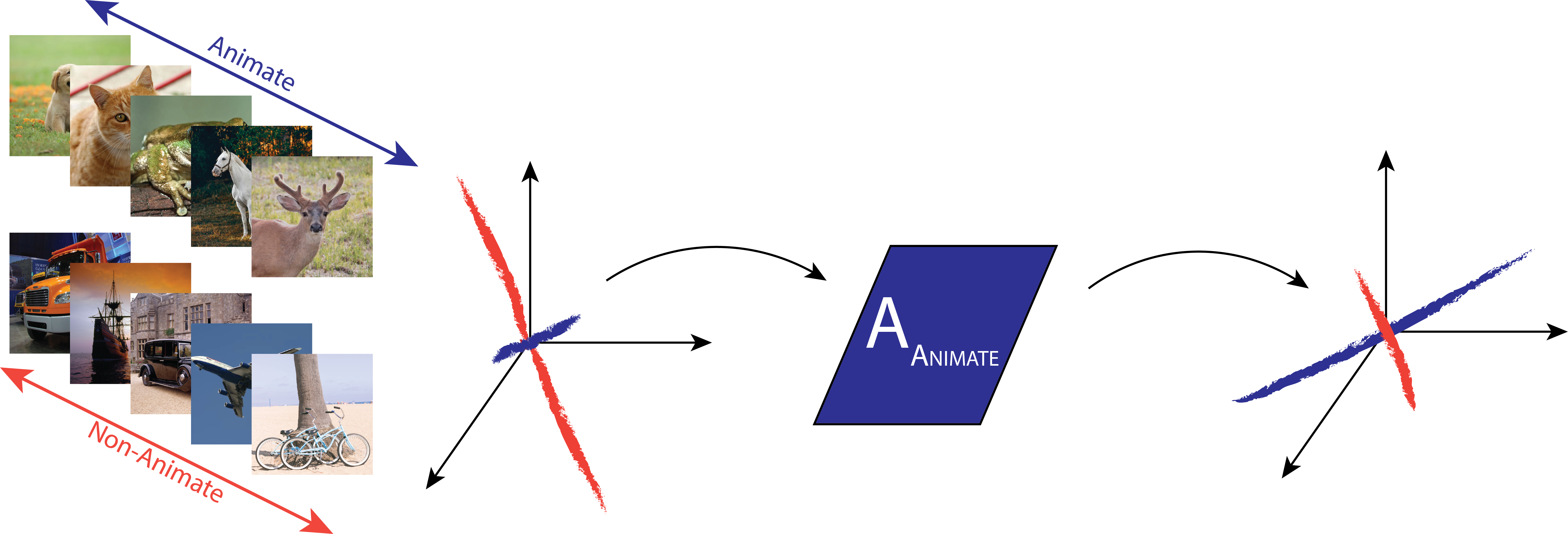
Figure 4: Illustration of the effect of affine transformation application over injection level features. Shown are images from two contexts, and the injection level feature representations for those contexts. If the dimension of the feature map of the injection level is HxWxC (Height x Width x Channel), this vector space is C-dimensional. The feature vectors are color coded according to context. After feature vector modulation through application of an affine transformation, the characteristics of the context associated with that affine transformation are more prominent. For example, with reference to Figure 1, if it is known that the context is one involving animals, rather than food, then characteristics may be biased towards fur interpretations, rather than kiwi fuzz or pastry surfaces.

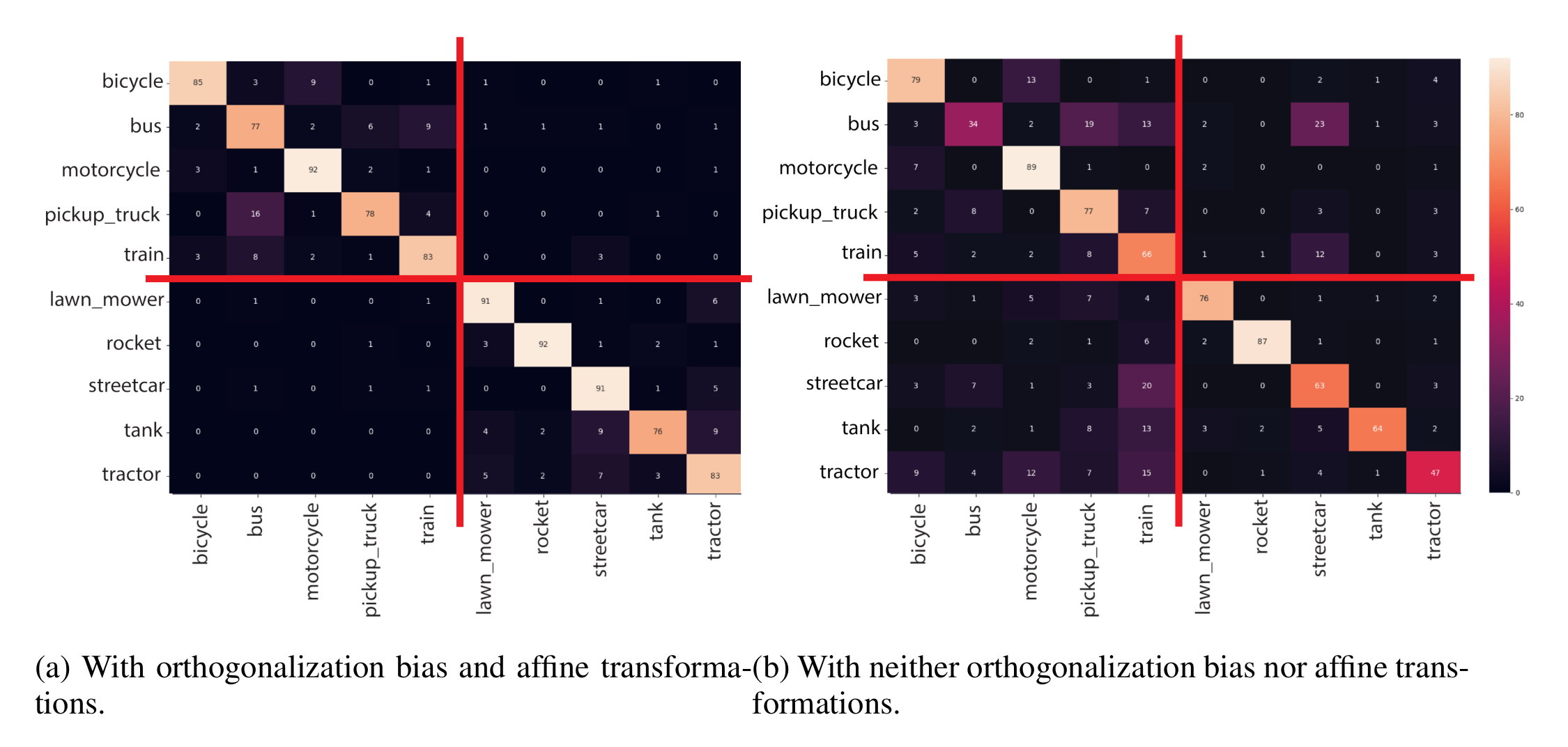
Figure 5: Confusion matrices for a our simple architecture (see Appendix ) with and without feedback (orthogonalization bias and with application of affine transformations) - subfigure a and b respectively - over the vehicles 1 vs vehicles 2 split of CIFAR100. The first 5 rows correspond to the first context, and the next 5 rows correspond to the second context. Note that cross context confusion (quadrants 1 and 3 of the confusion matrices) is significantly reduced with feedback.